Koyo Technical Information
a. Purpose and selection
The purpose of fit is to prevent harmful sliding between two mating bodies, by securely fastening a bearing ring, which rotates under loads, on the shaft or housing.
This harmful sliding is called creep. It may induce excessive heating, wear in the contact area of the mating surfaces, ingress of wear debris into the bearing, vibration, and other unwanted phenomena.
To determine what class of fit is optimal, examine the following:
1) The characteristics and sizes of loads
2) Temperature distribution during rotation
3) Bearing internal clearance
4) The material, finishing, and strength of the shaft and housing
5) Mounting and dismounting methods
6) Whether shaft thermal expansion needs to be accommodated between the mating surfaces of the fit
7) Bearing type and dimensions
b. Load characteristics
To prevent creeping, interference fit is used on the ring that is rotated. The table below shows the possible load combinations along with the classes of fit that is suitable for the individual combinations.
| Rotation pattern | Direction of load | Loading conditions | Fit | Typical application | |
|---|---|---|---|---|---|
| Inner ring & shaft |
Outer ring & housing |
||||
Inner ring : rotating Outer ring : stationary |
Stationary |
Rotating inner ring load Stationary outer ring load |
Interference fit necessary (k, m, n, p, r) |
Clearance fit acceptable (F, G, H, JS) |
Spur gear boxes, motors |
 Inner ring: stationary Outer ring: rotating |
Rotating with outer ring |
Greatly unbalanced wheels | |||
 Inner ring: stationary Outer ring: rotating |
Stationary |
Stationary inner ring load Rotating outer ring load |
Clearance fit acceptable (f, g, h, js) |
Interference fit necessary (K, M, N, P) |
Running wheels& pulleys with stationary shaft |
Inner ring: rotating Outer ring: stationary |
Rotating with inner ring |
Shaker screens unbalanced vibration) | |||
| Indeterminate | Rotating or stationary | Indeterminate direction load | Interference fit | Interference fit | Cranks |
c. Load magnitude
The inner ring contracts in the radial direction due to radial loads, while it expands in the circumferential direction. The interference at the time of assembly may, therefore, slightly decrease.
The decrease in the interference can be calculated by the following equations:
(In the case of Fr≤0.25Co)
![]()
(In the case of Fr>0.25Co)
![]()
| where: | ||
| ΔdF: | reduction of inner ring interference | mm |
| d: | bore diameter of bearing | mm |
| B: | inner ring width | mm |
| Fr: | radial load | N |
| Co: | basic static load rating | N |
d. Surface roughness
The effective interference obtained after fitting differs from calculated interference due to plastic deformation of the ring-fitting surface. When the inner ring is fitted, the effective interference, subject to the effect of the fitting surface finish, can be approximated by the following equations:
(In the case of a ground shaft)
Δdeff![]() Δd
Δd ![]() d/(d+2)
d/(d+2)
(In the case of a turned shaft)
Δdeff![]() Δd
Δd ![]() d/(d+3)
d/(d+3)
| where: | ||
| Δdeff | : effective interference | mm |
| Δd | : calculated interference | mm |
| d | : bore diameter of bearing | mm |
e. Temperature
The inner ring of a bearing rotating under loads may be heated beyond the temperature of the shaft. The thermal expansion of the ring may reduce effective interference.
Experiments have proved that the difference in temperature between the shaft and inner ring is equivalent to 10% to 15% of that between the inside bearing and housing periphery. The reduction in the interference due to the thermal expansion can be, therefore, calculated by the following equation:
| Δdt | =(0.10 to 0.15)Δt |
|
| where : | ||
| Δdt: | reduction of interference due to temperature difference | mm |
| Δt: | temperature difference between the inside of the bearing and the surrounding housing |
K |
| α: | linear expansion coefficient of bearing steel ( |
1/K |
| d: | bore diameter of bearing | mm |
f. Maximum stress of bearing
When a bearing ring is assembled with interference fit, a stress may be occurred as the ring expands or contracts.
If the stress is excessively large, the ring may break down.
If the ring is made from bearing steel, it is safe if the stress can be controlled at 120 MPa or less.
The maximum possible stress can be estimated by the following equations:
Maximum fitting – generated stress in bearings
| Shaft and inner ring | Housing bore and outer ring |
|---|---|
(In the case of hollow shaft)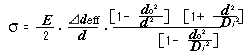 |
(In the case of Dh≠∞) |
| (In the case of solid shaft) |
(In the case of Dh=∞) |
| where : | |||||
| maximum stress | MPa | ||||
| d: | nominal bore diameter of inner ring(shaft diameter) | mm | |||
| Di: | raceway contact diameter of inner ring | mm | |||
| for ball bearing |
|||||
| for roller bearing |
|||||
| Δdeff: | effective interference of inner ring | mm | |||
| do: | bore diameter of hollow shaft | mm | |||
| De: | raceway contact diameter of outer ring | mm | |||
| for ball bearing |
|||||
| for roller bearing |
|||||
| D: | nominal outside diameter of outer ring (bore diameter of housing) |
mm | |||
| ΔDeff: | effective interference of outer ring | mm | |||
| Dh: | outside diameter of housing | mm | |||
| E: | young’s modulus 2.08×105 MPa | ||||
[Remark] The above equations are applicable when the shaft and housing are steel. When other materials are used, Koyo should be consulted.

 Exclusive North American distributor for Gamet Bearing.
Exclusive North American distributor for Gamet Bearing.